PPT I TRIANGOLI PowerPoint Presentation, free download ID2062189

annaci.best

La bisettrice come luogo geometrico YouTube

Considero un triangolo ABC qualsiasi. Traccio la bisettrice dell'angolo ^A A ^ che interseca il lato opposto BC nel punto D, dividendolo in due segmenti BD e CD. La bisettrice divide l'angolo al vertice A in due angoli di pari ampiezza α'≅α'' (congruenti). Devo dimostrare che il segmento BD sta a CD come AB sta a AC.

La bisettrice nel triangolo isoscele YouTube

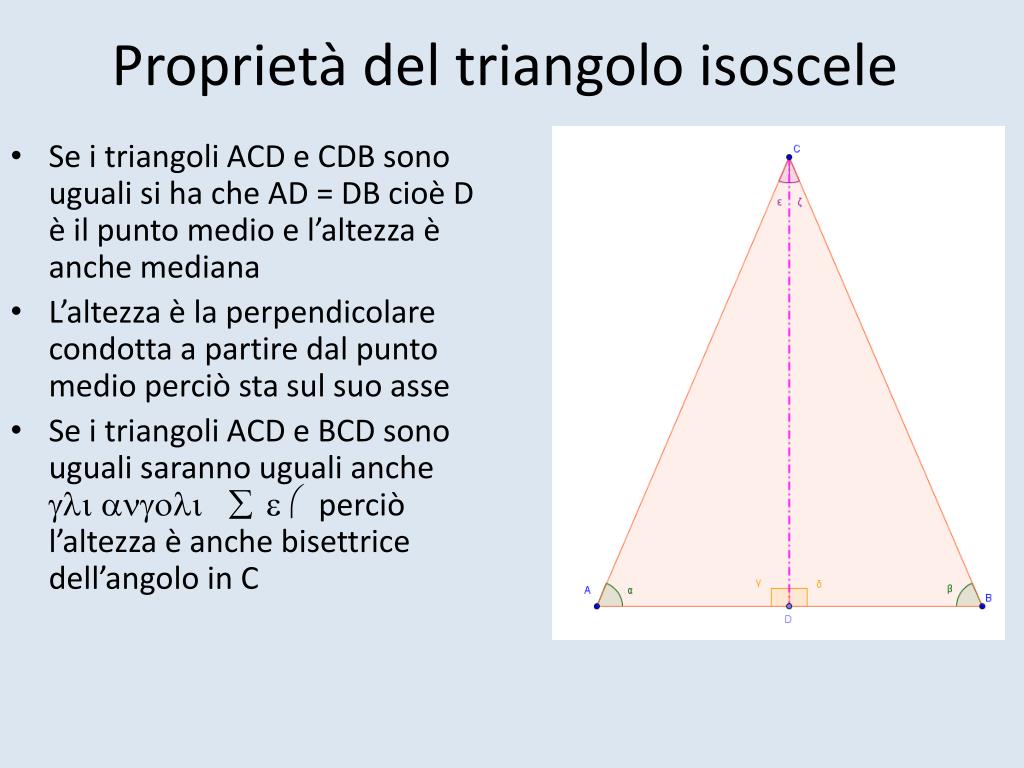
La bisettrice divide il triangolo in due triangoli rettangoli ACM e BCM che hanno: lo stesso lato CM. due lati congruenti AC≅BC. gli angoli tra i lati congruenti γ 1 ≅γ 2. Quindi, per il primo principio della congruenza, i triangoli AMC e BMC sono congruenti. AM C ≅BM C A M C ≅ B M C.

Triangolo Rettangolo Formule e Teoremi La risposta che cerchi

La bisettrice di un diedro ha la proprietà di essere il luogo dei punti equidistanti dai piani ai quali appartengono le facce del diedro. In un triangolo, la bisettrice di ogni suo angolo interno divide il lato opposto in segmenti proporzionali ai lati che lo comprendono ( teorema della bisettrice ).

BISETTRICI DI UN TRIANGOLO GeoGebra

Il teorema della bisettrice afferma che la bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due lati; detti A, B, C i vertici di un triangolo qualsiasi e AD la bisettrice dell'angolo in A, vale la proporzione CD:DB=AC:AB.

Paradiso delle mappe Altezza, mediana bisettrice del triangolo

Bisettrice di un angolo. La bisettrice di un angolo di un triangolo è il segmento che congiunge il vertice dell'angolo al lato opposto e che divide l'angolo in due parti uguali. In modo del tutto analogo si può definire anche la nozione di bisettrice di un angolo esterno.

La bisettrice di un angolo YouTube

Il teorema della bisettrice affferma che in un triangolo qualunque, la bisettrice di un suo angolo interno divide il lato opposto in segmenti proporzionali agli altri due lati. Stabilito ciò, completiamo la dimostrazione di questo enunciato con le restanti formule.

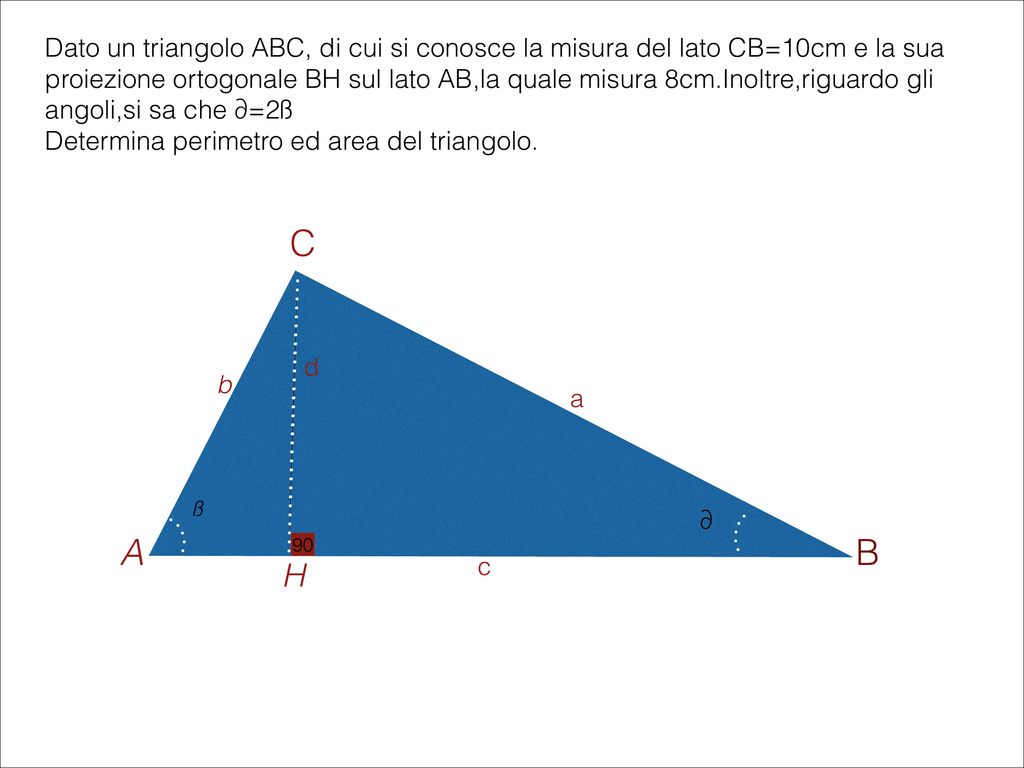
Dato un triangolo ABC, di cui si conosce la misura del lato CB=10cm

In geometria, si definisce bisettrice una retta od un piano che divide un'entità come ad esempio us segmento od un piano in due parti congruenti. Nello specifico, ci occuperemo di dividere un.

La bisettrice nei triangoli Appunti Per Tutti

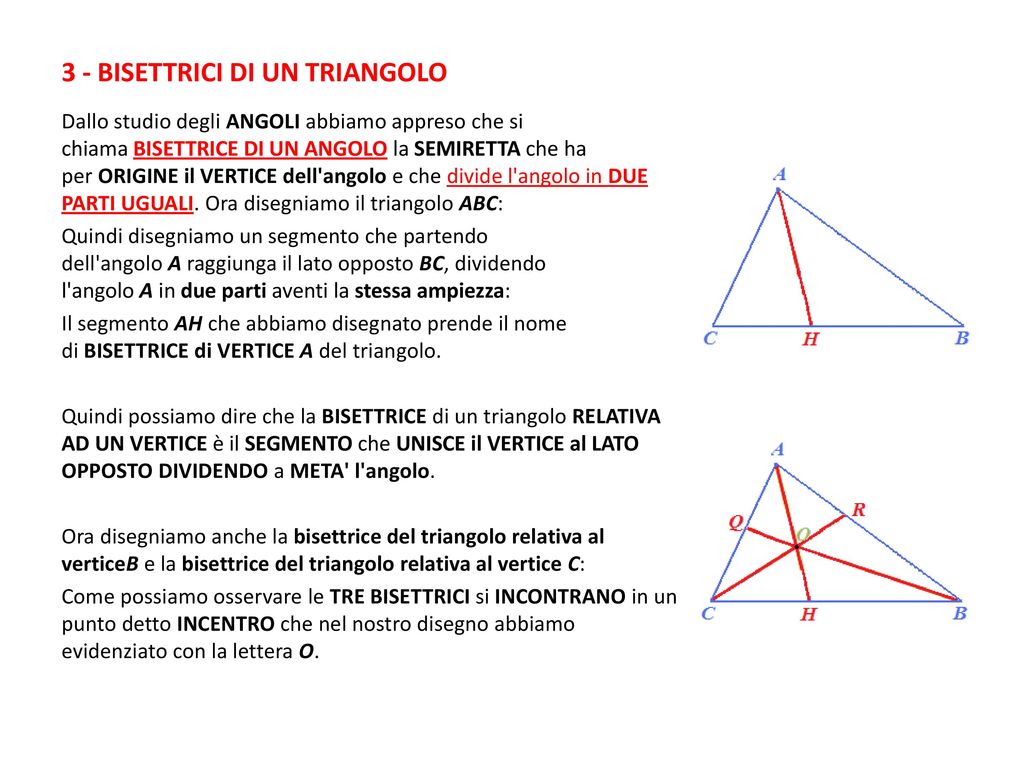
Sappiamo già che la bisettrice di un triangolo è la semiretta che divide l'angolo in due parti congruenti. Ora, dato il triangolo ABC, consideriamo i segmenti AD, BE, CF, cioè i segmenti delle bisettrici di A^, B^ e C^; questi segmenti si dicono bisettrici del triangolo relative ai vertici A, B, C. Possiamo quindi dare la seguente definizione:

Triangoli 5 Teorema della bisettrice del triangolo isoscele YouTube

La bisettrice di un triangolo è la semiretta che taglia l'angolo di un triangolo a metà. Consideriamo il triangolo ABC e il suo angolo di vertice A. La bisettrice dell'angolo Â si dice bisettrice del triangolo di vertice A. Quante sono le bisettrici di un triangolo?

Bisettrice di un triangolo e incentro geometria Studia Rapido

In un triangolo la bisettrice di un vertice è un segmento che divide un angolo in due parti congruenti e ha per estremi il vertice dell'angolo e un punto del lato opposto al vertice. Ogni triangolo ha tre bisettrici, una per ogni vertice. Ad esempio, considero un triangolo ABC.

GEOMETRIA PIANA. ppt scaricare

Definizione. La bisettrice di un angolo è il luogo dei punti del piano equidistanti dai lati dell'angolo. La bisettrice è dunque quella semiretta, con origine nel vertice dell'angolo, che lo divide in due parti uguali. Costruzione geometrica.

PPT I TRIANGOLI PowerPoint Presentation, free download ID2062189

Nel triangolo ABC, il cui lato BC è lungo cm 7, la bisettrice dell'angolo C interseca AB nel punto D distante cm 5 da B. Sapendo che AB*BC = AD^2 - DB^2, determinare il perimetro del triangolo ABC. [Risultato: 40.8]

G3 Teorema della Bisettrice dei Triangoli Isosceli. YouTube

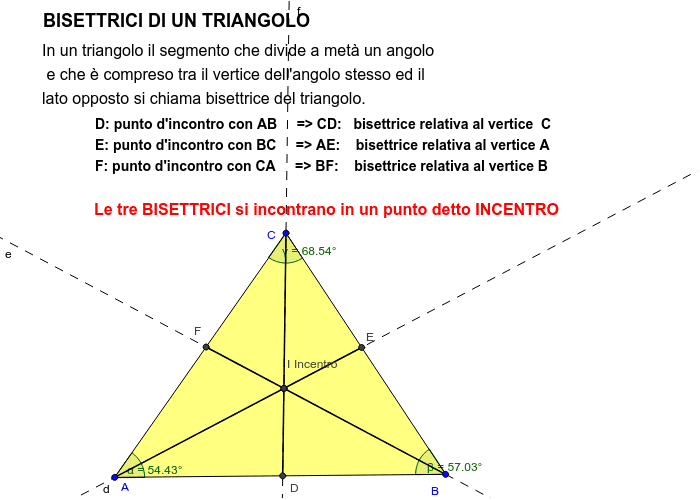
Possiamo riassumere e dire che: la bisettrice di un triangolo relativa a un angolo è il segmento che divide l'angolo compreso tra il vertice dell'angolo stesso e il lato opposto in due angoli uguali. Le tre bisettrici si incontrano in un punto detto incentro, che è sempre interno al triangolo ed equidistante dai tre lati.

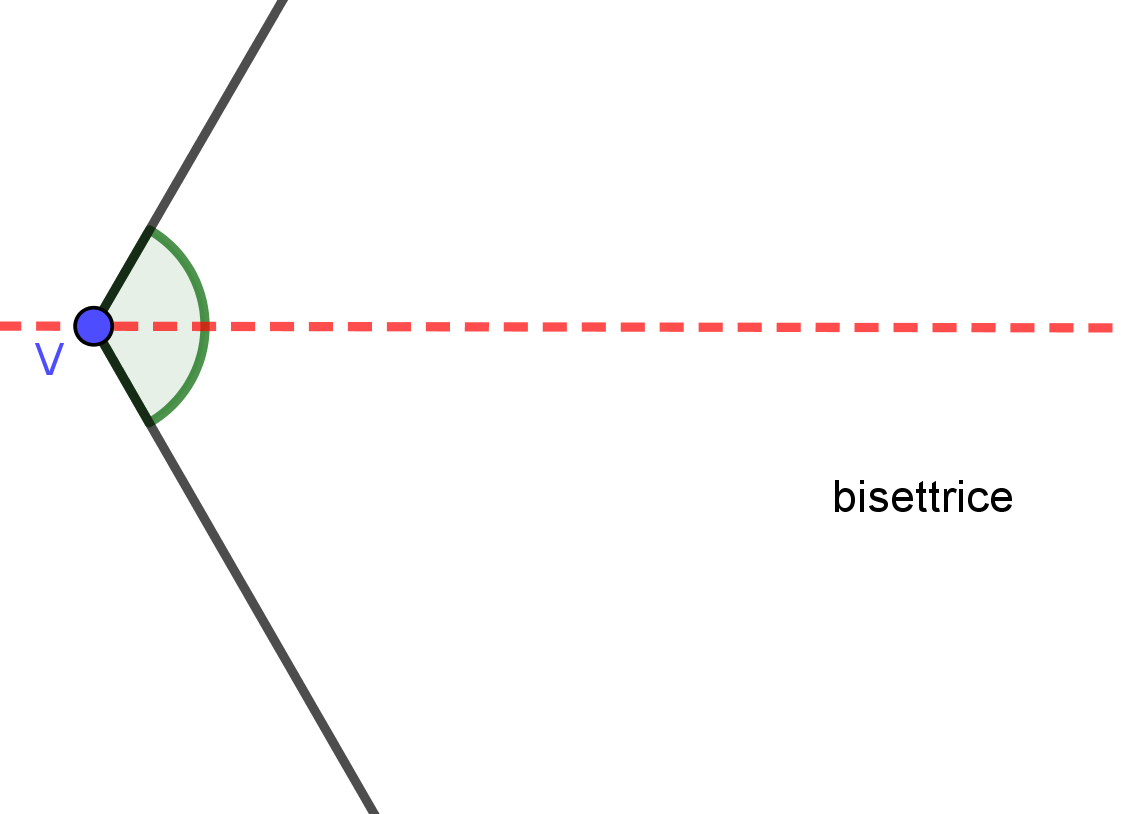
BISETTRICE DI UN ANGOLO lezioniignoranti

Indice. 1 Retta bisettrice. 2 Bisettrice dell'angolo. 2.1 Costruzione con riga e compasso. 2.1.1 Angolo concavo. 2.2 Proprietà. 2.2.1 Luogo dei punti equidistanti. 3 La bisettrice nel triangolo. 3.1 Teoremi legati alle bisettrici interne. 3.1.1 Primo teorema. 3.1.2 Teorema della bisettrice. 3.2 Formulario. 3.3 Teoremi legati alle bisettrici esterne

Punti Notevoli di un Triangolo

Quindi possiamo dire che la BISETTRICE di un triangolo RELATIVA AD UN VERTICE è il SEGMENTO che UNISCE il VERTICE al LATO OPPOSTO DIVIDENDO a META' l'angolo. Ora disegniamo anche la bisettrice del triangolo relativa al vertice B e la bisettrice del triangolo relativa al vertice C: Come possiamo osservare le TRE BISETTRICI si INCONTRANO in un.

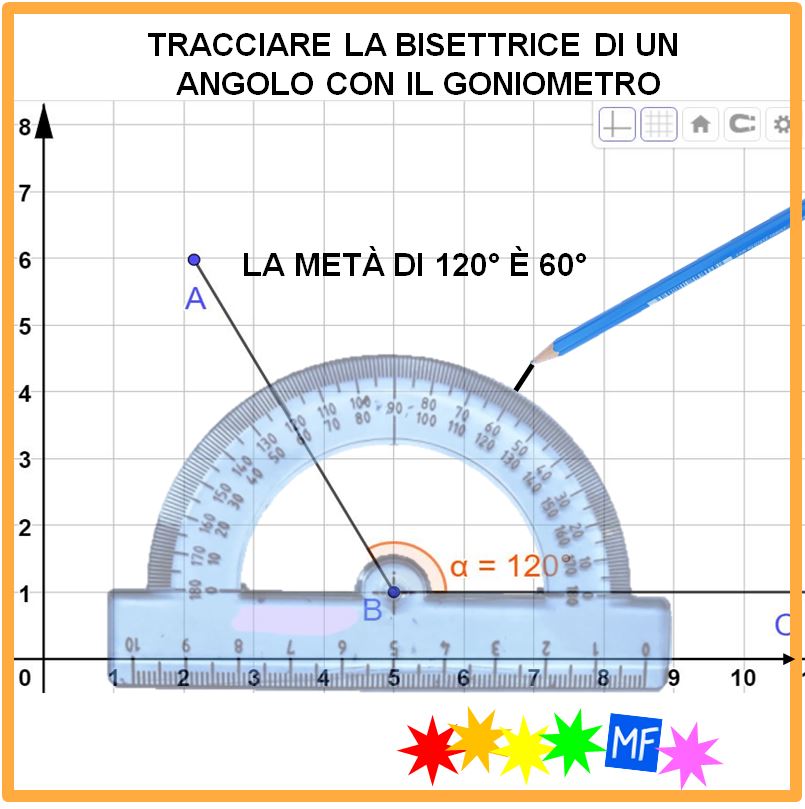
Come si disegna e cos'è una bisettrice Matematica Facile

La formula per ottenere l'altezza di un triangolo è la seguente. h = 2A b h = 2 A b. Dove A è l'area del triangolo e b la lunghezza della base. Quindi, per calcolare l'altezza del triangolo, basta dividere il doppio dell'area per la lunghezza della base. Nota.